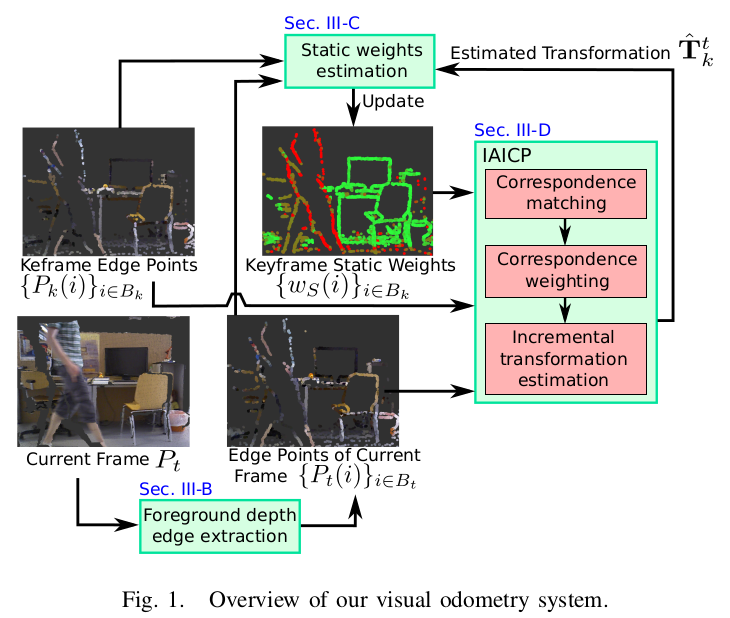
**Overview**
For each incoming frame, foreground edge points are first extracted, where only extracted edge
points are used for odometry estimation. Every Nth frame is selected as a keyframe . For each keyframe, static weights for edge points are estimated.
**A static weight indicates how likely one point belongs to the static environment.**
Then the relative transformation from the keyframe to the current frame is estimated using IAICP algorithm , where static weights are combined in order to reduce the effect of dynamic moving objects on the transformation estimation.
Finally, the static weights for the keyframe are updated based on the estimated motion.
**Foreground depth edge extraction**
Depth edge points are points that have large depth discontinuity in their neighourhood.
Two types of depth edge points exist: foreground edge points and occluded edgepoints. Foreground edge points present boundaries of objects, which are in front of other objects. Occluded edge points are from objects behind some other objects, they are caused by occlusion of other objects infront of them
However occluded edge points are sensitive to a moving camera, therefore they need to be excluded for estimating camera trajectory.
**Static weight estimation**
**Intensity Assisted Iterative Closest Point**
Correspondence weighting:
$W(i) = W_I(i) W_G(i) W_s(i)$
Using the proposed weighting terms, outlying correspondences with large **intensity** difference or having large **geometric** distance are intuitively downweighted. Furthermore, the **static weight** is responsible to downweight the influence of dynamic object.
Correspondence matching:
$s(i,j) = w_I (I_{src}(ind^{-1}(i)) - I_{tgt}(ind^{-1}(j)) w_G^{u=0} (||T^*P_{src}(i) - P_{tgt}(j) ||)$
Then the correspondence is taken as the point that maximizes the score function:
$c(i)=argmax s(i,j)$
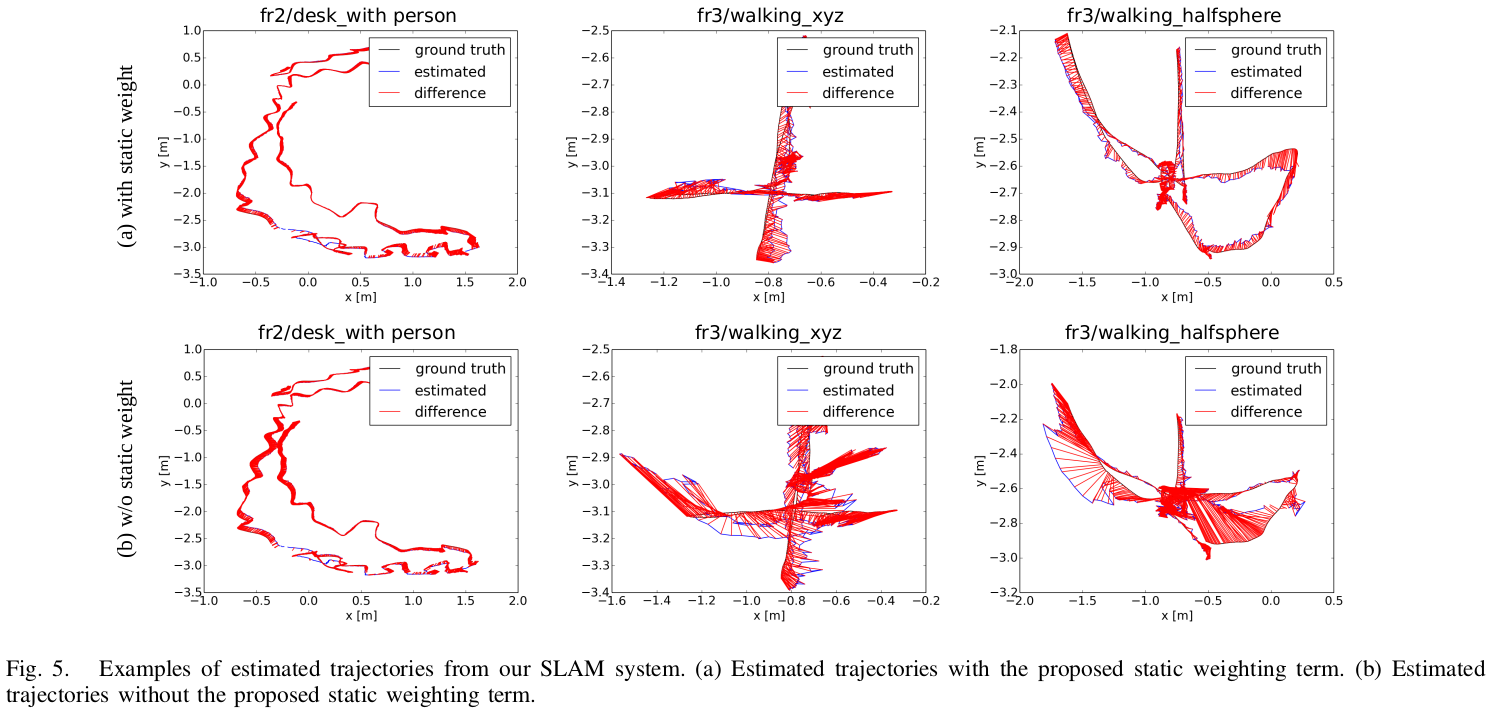
**Experiment**
# References
Li, S., & Lee, D. (2017). RGB-D SLAM in Dynamic Environments Using Static Point Weighting. IEEE Robotics and Automation Letters, 2(4), 2263–2270. https://doi.org/10.1109/LRA.2017.2724759
RGB-D SLAM in Dynamic Environments Using Static Point Weighting [Reading Seminar]
[toc]
# 2017 - RGB-D SLAM in Dynamic Environments Using Static Point Weighting
**contributions**:
• A novel efficient static weighting method is proposed to reduce the influence of dynamic objects on pose estimation. It calculates the likelihood of each keyframe point being part of the static environment.
• The static weighting terms are integrated into the IAICP method. This leads to a real-time RGB-D visual odometry method for dynamic environment.
**Overview**
For each incoming frame, foreground edge points are first extracted, where only extracted edge
points are used for odometry estimation. Every Nth frame is selected as a keyframe . For each keyframe, static weights for edge points are estimated.
**A static weight indicates how likely one point belongs to the static environment.**
Then the relative transformation from the keyframe to the current frame is estimated using IAICP algorithm , where static weights are combined in order to reduce the effect of dynamic moving objects on the transformation estimation.
Finally, the static weights for the keyframe are updated based on the estimated motion.
**Foreground depth edge extraction**
Depth edge points are points that have large depth discontinuity in their neighourhood.
Two types of depth edge points exist: foreground edge points and occluded edgepoints. Foreground edge points present boundaries of objects, which are in front of other objects. Occluded edge points are from objects behind some other objects, they are caused by occlusion of other objects infront of them
However occluded edge points are sensitive to a moving camera, therefore they need to be excluded for estimating camera trajectory.
**Static weight estimation**
**Intensity Assisted Iterative Closest Point**
Correspondence weighting:
$W(i) = W_I(i) W_G(i) W_s(i)$
Using the proposed weighting terms, outlying correspondences with large **intensity** difference or having large **geometric** distance are intuitively downweighted. Furthermore, the **static weight** is responsible to downweight the influence of dynamic object.
Correspondence matching:
$s(i,j) = w_I (I_{src}(ind^{-1}(i)) - I_{tgt}(ind^{-1}(j)) w_G^{u=0} (||T^*P_{src}(i) - P_{tgt}(j) ||)$
Then the correspondence is taken as the point that maximizes the score function:
$c(i)=argmax s(i,j)$
**Experiment**
# References
Li, S., & Lee, D. (2017). RGB-D SLAM in Dynamic Environments Using Static Point Weighting. IEEE Robotics and Automation Letters, 2(4), 2263–2270. https://doi.org/10.1109/LRA.2017.2724759
**Overview**
For each incoming frame, foreground edge points are first extracted, where only extracted edge
points are used for odometry estimation. Every Nth frame is selected as a keyframe . For each keyframe, static weights for edge points are estimated.
**A static weight indicates how likely one point belongs to the static environment.**
Then the relative transformation from the keyframe to the current frame is estimated using IAICP algorithm , where static weights are combined in order to reduce the effect of dynamic moving objects on the transformation estimation.
Finally, the static weights for the keyframe are updated based on the estimated motion.
**Foreground depth edge extraction**
Depth edge points are points that have large depth discontinuity in their neighourhood.
Two types of depth edge points exist: foreground edge points and occluded edgepoints. Foreground edge points present boundaries of objects, which are in front of other objects. Occluded edge points are from objects behind some other objects, they are caused by occlusion of other objects infront of them
However occluded edge points are sensitive to a moving camera, therefore they need to be excluded for estimating camera trajectory.
**Static weight estimation**
**Intensity Assisted Iterative Closest Point**
Correspondence weighting:
$W(i) = W_I(i) W_G(i) W_s(i)$
Using the proposed weighting terms, outlying correspondences with large **intensity** difference or having large **geometric** distance are intuitively downweighted. Furthermore, the **static weight** is responsible to downweight the influence of dynamic object.
Correspondence matching:
$s(i,j) = w_I (I_{src}(ind^{-1}(i)) - I_{tgt}(ind^{-1}(j)) w_G^{u=0} (||T^*P_{src}(i) - P_{tgt}(j) ||)$
Then the correspondence is taken as the point that maximizes the score function:
$c(i)=argmax s(i,j)$
**Experiment**
# References
Li, S., & Lee, D. (2017). RGB-D SLAM in Dynamic Environments Using Static Point Weighting. IEEE Robotics and Automation Letters, 2(4), 2263–2270. https://doi.org/10.1109/LRA.2017.2724759
No comments